Property B
In mathematics, Property B is a certain set theoretic property. Formally, given a finite set X, a collection C of subsets of X, all of size n, has Property B if we can partition X into two disjoint subsets Y and Z such that every set in C meets both Y and Z. The smallest number of sets in a collection of sets of size n such that C does not have Property B is denoted by m(n).
The property gets its name from mathematician Felix Bernstein, who first introduced the property in 1908.
Values of m(n)
It is known that m(1) = 1, m(2) = 3, and m(3) = 7 (as can by seen by the following examples); the value of m(4) is not known, although an upper bound of 23 (Seymour, Toft) and a lower bound of 21 (Manning) have been proven. At the time of this writing (August 2004), there is no OEIS entry for the sequence m(n) yet, due to the lack of terms known.
- m(1)
- For n = 1, set X = {1}, and C = {{1}}. Then C does not have Property B.
- m(2)
- For n = 2, set X = {1, 2, 3} and C = {{1, 2}, {1, 3}, {2, 3}}. Then C does not have Property B, so m(2) <= 3. However, C' = {{1, 2}, {1, 3}} does (set Y = {1} and Z = {2, 3}), so m(2) >= 3.
- m(3)
- For n = 3, set X = {1, 2, 3, 4, 5, 6, 7}, and C = {{1, 2, 4}, {2, 3, 5}, {3, 4, 6}, {4, 5, 7}, {5, 6, 1}, {6, 7, 2}, {7, 1, 3}} (the Steiner triple system S7); C does not have Property B (so m(3) <= 7), but if any element of C is omitted, then that element can be taken as Y, and the set of remaining elements C' will have Property B (so for this particular case, m(3) >= 7). One may check all other collections of 6 3-sets to see that all have Property B.
- m(4)
- Seymour (1974) constructed a hypergraph on 11 vertices with 23 edges withouth Property B, which shows that m(4) <= 23. Manning (1995) proved that m(4) >= 20.
Asymptotics of m(n)
Erdős (1963) proved that for any collection of fewer than 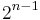 sets of size n, there exists a 2-coloring in which no set is monochromatic. The proof is simple: Consider a random coloring. The probability that any one set is monochromatic is
sets of size n, there exists a 2-coloring in which no set is monochromatic. The proof is simple: Consider a random coloring. The probability that any one set is monochromatic is 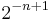 . By a union bound, the probability that any set is monochromatic is less than
. By a union bound, the probability that any set is monochromatic is less than 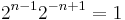 . Therefore, there exists a good coloring.
. Therefore, there exists a good coloring.
Erdős (1964) constructed an n-uniform graph with 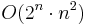 edges which does not have property B, establishing an upper bound. Schmidt (1963) proved that every collection of at most
edges which does not have property B, establishing an upper bound. Schmidt (1963) proved that every collection of at most 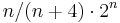 has property B. Erdős and Lovász conjectured that
has property B. Erdős and Lovász conjectured that 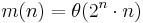 . Beck in 1978 improved the lower bound to
. Beck in 1978 improved the lower bound to 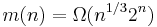 . In 2000, Radhakrishnan and Srinivasan improved the lower bound to
. In 2000, Radhakrishnan and Srinivasan improved the lower bound to 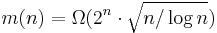 . They used a clever probabilistic algorithm.
. They used a clever probabilistic algorithm.
References
- Bernstein, F. (1908), "Zur theorie der trigonometrische Reihen", Leipz. Ber. 60: 325–328.
- Erdős, Paul (1963), "On a combinatorial problem", Nordisk Mat. Tidskr. 11: 5–10
- Erdős, P. (1964). "On a combinatorial problem. II". Acta Mathematica Academiae Scientiarum Hungaricae 15 (3–4): 445–447. doi:10.1007/BF01897152.
- Schmidt, W. M. (1964). "Ein kombinatorisches Problem von P. Erdős und A. Hajnal". Acta Mathematica Academiae Scientiarum Hungaricae 15 (3–4): 373–374. doi:10.1007/BF01897145.
- Seymour, Paul (1974), "A note on a combinatorial problem of Erdős and Hajnal", Bull. London Math. Soc. (2) 8: 681–682, doi:10.1112/jlms/s2-8.4.681.
- Toft, Bjarne (1975), "On colour-critical hypergraphs", in Hajnal, A.; Rado, Richard; Sós, Vera T., Infinite and Finite Sets: To Paul Erdös on His 60th Birthday, North Holland Publishing Co., pp. 1445–1457.
- Manning, G. M. (1995), "Some results on the m(4) problem of Erdős and Hajnal", Electron. Research Announcements of the American Mathematical Society 1: 112–113, doi:10.1090/S1079-6762-95-03004-6.
- Beck, J. (1978), "On 3-chromatic hypergraphs", Discrete Mathematics 24 (2): 127–137, doi:10.1016/0012-365X(78)90191-7.
- Radhakrishnan, J.; Srinivasan, A. (2000), "Improved bounds and algorithms for hypergraph 2-coloring", Random Structures and Algorithms 16 (1): 4–32, doi:10.1002/(SICI)1098-2418(200001)16:1<4::AID-RSA2>3.0.CO;2-2, http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=00743519.
- Miller, E. W. (1937), "On a property of families of sets", Comp. Rend. Varsovie: 31–38.
- Erdős, P.; Hajnal, A. (1961), "On a property of families of sets", Acta Math. Acad. Sci. Hung. 12: 87–123, doi:10.1007/BF02066676.
- Abbott, H. L.; Hanson, D. (1969), "On a çombinatorial problem of Erdös", Canad. Math. Bull. 12: 823–829, doi:10.4153/CMB-1969-107-x
.